|
What is the NMR Restraints Grid?
The NMR Restraints Grid contains the original NMR data as collected for over 2500
protein and nucleic acid structures with corresponding PDB entries.
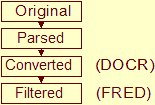
In addition to the original restraints, most of the distance, dihedral angle and RDC restraint data (>85%)
were parsed, and those in over 500 entries were converted
and filtered. The converted and filtered data sets constitute the
DOCR and FRED databases respectively as described in these
references.
For tips on using this interface and how to link to it, check the
howto.
A block is a section of data of similar type such as hydrogen bond distance restraints or RDCs.
|